JEE Main is one of the toughest competitive examinations in the country. A lot of hard work is required to clear this examination. The best way to score well in the examination is by solving previous years’ question papers and taking mock tests regularly. JEE Main 2020 Mathematics (January 8, Shift 1) is solved on this page.

January 8 Shift 1 - Maths

1. For which of the following ordered pairs (?, ?), the system of linear equations

? + 2? + 3? = 1

3? + 4? + 5? = ?

4? + 4? + 4? = ?

is inconsistent?

a. (4, 6)
b. (3, 4)
c. (1, 0)
d. (4, 3)

Solution:

D =

$\begin{vmatrix} 3 & 4 & 5\\ 1& 2 & 3\\ 4 & 4 & 4 \end{vmatrix}$

?₃ → ?₃ − 2?₁ + 2?₂

D =

$\begin{vmatrix} 3 & 4 & 5\\ 1& 2 & 3\\ 0 & 0 & 0 \end{vmatrix}$

For inconsistent system, one of ?_?, ?_?, ?_? should not be equal to 0

Dx =

$\begin{vmatrix} \mu & 4 & 5\\ 1& 2 & 3\\ \delta & 4 & 4 \end{vmatrix}$

Dy =

$\begin{vmatrix} 3 & \mu & 5\\ 1& 2 & 3\\ 4 & \delta & 4 \end{vmatrix}$

Dz =

$\begin{vmatrix} 3 & 4 & \mu \\ 1& 2 & 1\\ 4 & 4 & \delta \end{vmatrix}$

For inconsistent system, 2? ≠ ? + 2

∴ The system will be inconsistent for ? = 4, ? = 3.

2. Let ? = (?) be a solution of the differential equation,

$\sqrt{1-x^{2}}\frac{dy}{dx}+\sqrt{1-y^{2}}=0,\left | x \right |< 1$

.If y (1/2) = √3/2, then y(-1/√2) is equal to

a. -1/√2
b. -√3/2
c. 1/√2
d. √3/2

Solution:

$\sqrt{1-x^{2}}\frac{dy}{dx}+\sqrt{1-y^{2}}=0,$

$\frac{dy}{\sqrt{1-y^{2}}}+ \frac{dx}{\sqrt{1-x^{2}}}=0$

sin^-1y ₊sin^-1x = c

If x = ½, y = √3/2 then,

sin^-1(√3/2) + sin^-1(1/2) = c

(π/3) +(π/6) = c

Therefore, c = π/2

sin^-1y = π/2 - sin^-1x = cos^-1x

sin^-1y = cos^-1(1/√2)

sin^-1y = π/4

y(1/√2)) = 1/√2)

3. If ?, ? and ? are the greatest values of ¹⁹?_?, ²⁰?_?, ²¹?_? respectively, then:

a. (a/11) = (b/22) = (c/42)
b. (a/10) = (b/11) = (c/42)
c. (a/11) = (b/22) = (c/21)
d. (a/10) = (b/11) = (c/21)

Solution:

Therefore, max (¹⁹C_p) = (¹⁹C₉) = a

max (²⁰C_p) = ²⁰C₁₀= b

max (²⁰C_r) = ²¹C₁₁= c

4. Which of the following is a tautology?

a. (? ∧ (? ⟶ ?)) ⟶ ?
b. ? ∧ (? ∨ ?)
c. (? → ( ∧ (? → ?))
d. ? ∨ (? ∧ ?)

Solution:

(? ∧ (? ⟶ ?)) ⟶ ?

= (? ∧ (∽ ? ∨ ?)) ⟶ ?

= [(? ∧∼ ?) ∨ (? ∧ ?)] ⟶ ?

= ? ∧ ? ⟶ ?

=∼ (? ∧ ?) ∨ ?

=∼ ? ∨∼ ? ∨ ?

= ?

5. Let ?: ? → ? be such that for all ? ∈ ?, (2^1+? + 2^1−?), f(?) and (3^? + 3^−?) are in A.P., then the minimum value of f(?) is:

a. 0
b. 4
c. 3
d. 2

Solution:

2^1−? + 2^1+?, (?), 3^? + 3^−? are in A.P.

$f(x)=\frac{3^{x}+3^{-x}+2^{1+x}+2^{1-x}}{2}=\frac{3^{x}+3^{-x}}{2}+\frac{2^{1+x}+2^{1-x}}{2}$

Also, Applying A.M. ≥ G.M. inequality, we get

$\frac{3^{x}+3^{-x}}{2} \geq \sqrt{3^{x}3^{-x}}$

$\frac{3^{x}+3^{-x}}{2} \geq 1$
-------- (1)

Applying A.M. ≥ G.M. inequality, we get

$\frac{2^{1+x}+2^{1-x}}{2}\geq \sqrt{2^{1+x}\times 2^{1-x}}$

$\frac{2^{1+x}+2^{1-x}}{2}\geq 2$
-------- (2)

Adding (1) and (2), we get

f(?) ≥ 1 + 2 = 3

Thus, minimum value of f(?) is 3.

6. The locus of a point which divides the line segment joining the point (0, −1) and a point on the parabola, ?² = 4?, internally in the ratio 1: 2, is:

a. 9?² − 12? = 8
b. 4?² − 3? = 2
c. ?² − 3? = 2
d. 9?² − 3? = 2

Solution:

Let point ? be (2?, ?²) and ? be (ℎ, ?).

$h=\frac{2t}{3},k=\frac{-2+t^{2}}{3}$

Now, eliminating ? from the above equations we get:

3k+2 = (3h/2)²

Replacing ℎ and ? by ? and ?, we get the locus of the curve as 9?² − 12? = 8.

7. For ? > 0, let the curves ?₁: ?² = ?? and ?₂ ∶ ?² = ?? intersect at origin ? and a point ?. Let the line ? = ? (0 < ? < ?) intersect the chord ?? and the ?-axis at points ? and ?, respectively. If the line x = b bisects the area bounded by the curves, C₁ and C₂ , and the area of Δ???=1/2,then‘a’ satisfies the equation

a. ?⁶ − 12?³ + 4 = 0
b. ?⁶ − 12?³ − 4 = 0
c. ?⁶ + 6?³ − 4 = 0
d. ?⁶ − 6?³ + 4 = 0

Solution:

Given, (Δ???)=1/2

⟹ 1/2×?×?=1/2

⇒?=1

As per the question

$\int_{0}^{1}\left ( \sqrt{ax} - \frac{x^{2}}{a}\right )dx= \frac{1}{2}\int_{0}^{a}\left ( \sqrt{ax} - \frac{x^{2}}{a}\right )dx$

(2/3)√a – (1/3a) = a²/6

2?√?−1=?³/2

⇒4?√?=2+?³

⇒16?³=4+?⁶+4?³

⇒?⁶−12?³+4=0

8.The inversion function of f(x) =

$\frac{8^{2x}-8^{-2x}}{8^{2x}+8^{-2x}},x \epsilon (-1,1), is$

Solved Question paper of JEE Main 2020 Maths

Solution:

$f(x) = \frac{8^{2x}-8^{-2x}}{8^{2x}+8^{-2x}} = \frac{8^{4x-1}}{8^{4x+1}}$

Put, y =
$\frac{8^{4x-1}}{8^{4x+1}}$

Applying componendo-dividendo on both sides

$\frac{y+1}{y-1}=\frac{2\times 8^{4x}}{-2}$

8^4x = (1+y)/(1-y)

$\lim_{x\rightarrow 0}\left ( \frac{3x^{2}+2}{7x^{2}+2} \right )^{1/x^{2}}$

is equal to

a. e
b. 1/e²
c. 1/e
d. e²

Solution:

Let,L=
$\lim_{x\rightarrow0}\left(\frac{3x^{2}+2}{7x^{2}+2}\right)^{1/x^{2}}$
(intermediate from 1^∞)

$L = e^{\lim_{x\rightarrow 0}\frac{1}{x^{2}}\left ( \frac{3x^{2}+2}{7x^{2}+2} -1\right )}$

$L = e^{\lim_{x\rightarrow 0}\frac{1}{x^{2}}\left ( \frac{-4x^{2}}{7x^{2}+2}\right )}$

= 1/e²

10. Let f(?) = (sin(tan⁻¹ ?) + sin(cot⁻¹ ?) )² − 1, where |?| > 1.

$\frac{dy}{dx}=\frac{1}{2}\frac{d}{dx}(sin^{-1}f(x)))$

and y(√3) = π/6, then y(-(√3) is equal to:

a. π/3
b. 2π/3
c. - π/6
d. 5 π/6

Solution:

f(?) = [sin(tan⁻¹ ?) + sin(cot⁻¹ ?) ]² -1

Put tan⁻¹ ? = ?, where ? ∈ (− π/2, - π/4) ᵁ (π/4, π/2)

= [sin(tan⁻¹ ?) + sin(cot⁻¹ ?) ²-1 = [sin ?+cos ?]²-1

= 1+2sin ?cos ? -1 = sin2? = (2x/1+x²)

It is given that
$\frac{dy}{dx}=\frac{1}{2}\frac{d}{dx}(sin^{-1}f(x)))$

$\frac{dy}{dx}=-\frac{1}{1+x^{2}},for \left | x \right |> 1$

⇒ x>1 and x<-1

To get the value of (−√3), we have to integrate the value of dy/dx. To integrate the expression, the

interval should be continuous. Therefore, we have to integrate the expression in both the intervals.

⇒ ? = −tan⁻¹ ? + ?₁ , for ? > 1 and ? = − tan⁻¹ ? + ?₂, for ? < −1

For ? > 1,C₁ =π/2

Since y(√3) = π/6 is given.

But ?₂ can’t be determined as no other information is given for ? < −1. Therefore, all the options can be true as ?₂ can’t be determined.

11. If the equation, ?² + ?? + 45 = 0 (? ∈ ?) has conjugate complex roots and they satisfy |? + 1| = 2√10 , then :

a. ?² + ? = 12
b. ?² − ? = 42
c. ?² − ? = 30
d. ² + ? = 72

Solution:

Given ?² + ?? + 45 = 0, ? ∈ ?, let roots of the equation be ? ± ??

Then, sum of roots = 2? = −?

Product of roots = ?² + ?² = 45

As ? ± ?? lies on |? + 1| = 2√10, we get

(? + 1)² + ?² = 40

⇒ ?² + ?² + 2? + 1 = 40

⇒ 45 − ? + 1 = 40

⇒ ? = 6

⇒ ?² − ? = 30.

12. The mean and standard deviation (s.d.) of 10 observations are 20 and 2 respectively. Each of these 10 observations is multiplied by ? and then reduced by ?, where ? ≠ 0 and ? ≠ 0. If the new mean and standard deviation become half of their original values, then ? is equal to:

a. −20
b.−5
c. 10
d.−10

Solution:

If mean ?̅ is multiplied by ? and then ? is subtracted from it, then new mean
$\bar{x}'= p\bar{x}-q$

$\bar{x}'= \frac{1}{2}\bar{x}$

And x= 10

⇒ 10 = 20 p –q--------(1)

If standard deviation is multiplied by ?, new standard deviation (?^′) is |?| times of the initial standard deviation (?).

$\sigma ' = \left | p \right |\sigma$

⇒
$\frac{1}{2}\sigma = \left | p \right |\sigma$

$\left | p \right |=1/2$

If p =1/2 ,q = 0

If p = -1/2 , q = -20

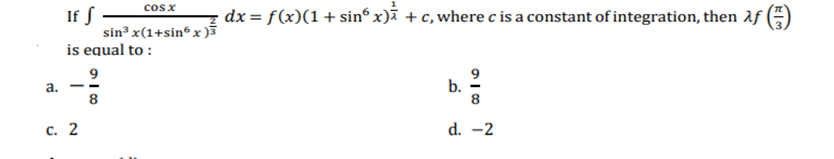
13. JEE Main Mathematics 2020 Shift 1 Jan 8 solved paper

Solution:

14. Let ? and ? be two independent events such that P(?) =1/3 and P(?) = 1/6. Then, which of the following is TRUE ?

a. P(?/(? ∪ ?)) = 1/4
b. P(?/?′) = 1/3
c. P(?/?) = 2/3
d. P(A′/B′) = 1/3

Solution:

If ? and ? are independent events, then

$P\left ( \frac{X}{Y} \right )=\frac{P(X\bigcap Y)}{P(Y)}$

$=\frac{P(X)P(Y)}{P(Y)}=P(X)$

Therefore,P(A/B) = P(A) = 1/3

⇒ P(A/B′) = P(A) = 1/3

15. If volume of parallelepiped whose coterminous edges are given by

$\vec{u} = \hat{i}+\hat{j}+\lambda \hat{k}$

$\hat{v}==\hat{i}+\hat{j}+3\hat{k} $

and

$\vec{w}=2\hat{i}+\hat{j}+\hat{k}$

be 1 cu. unit. If ? be the angle between the edges

$\vec{u}$

and

$\vec{w}$

then, cos ? can be:

a. 7/(6√6)
b. 5/7
c. 7/(6√3)
d. 5/(3√3)

Solution:

Volume of parallelepiped =
$\begin{bmatrix} \vec{u} &\vec{v} & \vec{w} \end{bmatrix}$

⇒
$\begin{vmatrix} 1 & 1& \lambda \\ 1& 1 & 3\\ 2& 1 & 1 \end{vmatrix}=\pm 1$

⇒ ? = 2 or 4

For ? = 4,

$cos\theta =\frac{2+1+4}{\sqrt{6}\sqrt{18}}=\frac{7}{6\sqrt{3}}$

16. Let two points be A(1, −1) and B(0, 2). If a point P(?′, ?′) be such that the area of ΔP?? = 5 sq.

units and it lies on the line, 3? + ? − 4? = 0, then the value of ? is :

a. 4
b. 1
c. −3
d. 3

Solution:

Area of triangle is

$A=\frac{1}{2}\begin{vmatrix} 1 & -1 & 1\\ 0 & 2 & 1\\ x' & y' & 1 \end{vmatrix}=\pm 5$

⇒
$\Rightarrow (2-y')-x'-2x'=\pm 10$

$\Rightarrow -3x'-y'+2=\pm 10$

3x’+y’=12 or 3x’+y’=-8

⇒ ? = 3 or −2

17. The shortest distance between the lines

$\frac{x-3}{3}=\frac{y-8}{-1}=\frac{z-3}{1}$

And

$\frac{x+3}{3}=\frac{y+7}{2}=\frac{z-6}{1}$

a. 2√30
b. (7/2)√30
c. 3
d. 3√30

Solution:

$\vec{AB}=-3\hat{i}-7 \hat{j}+6\hat{k}-(3\hat{i}+8\hat{j}+3\hat{k})=-6\hat{i}-15\hat{j}+3\hat{k}$

$\vec{p}=-3\hat{i}-\hat{j}+\hat{k}$

$\vec{q}=-3\hat{i}+\hat{2j}+\hat{4k}$

$\vec{p}\times \vec{q}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 3 &-1 & 1\\ -3 & 2 & 4 \end{vmatrix}=-6\hat{i}-15\hat{j}+\hat{9k}$

Shortest distance =
$\frac{\left | \vec{AB} (\vec{p}\times \vec{q})\right |}{\left | \vec{p}\times \vec{q} \right |}$

=
$\frac{\left | 36+225+9\right |}{\sqrt{36+225+9}}=3\sqrt{30}$

18. Let the line ? = ?? and the ellipse 2?² + ?² = 1 intersect a point ? in the first quadrant. If the normal to this ellipse at ? meets the co-ordinate axes at (−1/3√2,0) and (0, ?), then ? is equal to

a. 2/√3
b. 2/3
c. 2√2/3
d. √2/3

Solution:

Let ? ≡ (?₁, ?₁)

2?² + ?² = 1 is given equation of ellipse.

⇒ 4? + 2??’=0

⇒ ?′|_(?1,?1)= −2?₁/?₁

Therefore, slope of normal at (?₁, ?₁) is ?₁/2?₁

Equation of normal at (?₁, ?₁) is

(? − ?₁) = (?₁/2?₁) (? − ?₁)

It passes through (−1/3√2, 0)⇒ −?₁ = ?₁/2?₁(−1/3√2− ?₁)

⇒ ?₁ =1/3√2

⇒ ?₁ =2√2/3

as ? lies in first quadrant

Since (0, ?) lies on the normal of the ellipse at point ?, hence we get

? =?₁/2

=√2/3

19. If ? is a point at which Rolle’s theorem holds for the function, f(?) =

$log_{e}\left ( \frac{x^{2} + \alpha }{7x} \right )$

in the interval [3, 4], where ? ∈ ?, then ?′′(?) is equal to :

a. −1/24
b. −1/12
c. √3/7
d. 1/12

Solution:

Rolle’s theorem is applicable on f(?) in [3, 4]

⇒ f(3) = f(4)

⇒ l
$In\left ( \frac{9 + \alpha }{21} \right ) = In \left ( \frac{16+\alpha }{28} \right )$

⇒9 + ?/21 =16 + ?/28

⇒ 36 + 4? = 48 + 3? ⇒ ? = 12

Now, f(?) = ln ((?²+12)/7?) ⇒ ?′(?) =[7?/(?²+12)] ×(7?×2?−(?²+12)×7)/(7?)²

?′(?) =(?² – 12)/(?(?² + 12))

?′(?) = 0 ⇒ ? = 2√3

?′′(?) =(−?⁴ + 48?² + 144)/?²(?² + 12)²

∴ ?′′(?) =1/12

20. Let f(?) = ? cos⁻¹ (sin(−|?|)) , ? ∈ (− ?/2 , ?/2 ), then which of the following is true ?

a. ? ′ (0) = − ?/2
b. ? ′ is decreasing in (− ?/2 , 0) and increasing in (0, ?/2 )
c. ? is not differentiable at ? = 0
d. ? ′ is increasing in (− ?/2 , 0) and decreasing in (0, ?/2 )

Solution:

f(?) = ? cos⁻¹ (sin(−|?|))

⇒ f(?) = ? cos⁻¹ (− sin |?|)

⇒ f(?) = [? − cos⁻¹ (sin |?|)]

⇒ f(?) = ? [? − (?/2 − sin⁻¹ (sin |?|))]

⇒ f(?) = ? ( ?/2 + |?|)

21. An urn contains 5 red marbles, 4 black marbles and 3 white marbles. Then the number of ways in which 4 marbles can be drawn so that at most three of them are red is.

Solution:

Number of ways to select at most 3 red balls = P(0 red balls) +P(1 red ball) + ?(2 red balls ) + P(3 red balls)

= ⁷?₄ + ⁵?₁ × ⁷?₃ + ⁵?₂ × ⁷?₂ + ⁵?₃ × ⁷?₁

= 35 + 175 + 210 + 70 = 490

22. Let the normal at a ? on the curve ?² − 3?² + ? + 10 = 0 intersect the y-axis at (0,3/2). If ? is the slope of the tangent at ? to the curve, then |?| is equal to____________.

Solution:

Let co-ordinate of ? be (?¹, ?¹)

Differentiating the curve w.r.t ?

2??′ − 6? + ?′ = 0

Slope of tangent at ?

⇒ ?′ =6?₁/(1 + 2?₁)

?_normal=(( ?₁−3/2)/(?₁−0) )

∵ ?_normal×?_tangent= −1

⇒ ((3/2) − ?₁/−?₁)×(6?₁/1+2?₁) =−1

⇒?₁=1

⇒?₁=±2

Slope of tangent =±12/3 = ±4

⇒|?|=4

23. The least positive value of ′?′ for which the equation, 2?²+(?−10)?+(33/2) =2? has real roots is ____________.

Solution:

∵2?²+(?−10)?+33/2=2?, ? ∈ ?+ has real roots

⇒?≥0 ⇒(?−10)²−4×2×((33/2)−2?)≥0

⇒(?−10)²−4(33−4?)≥0

⇒a²−4?−32≥0

⇒?∈(−∞,−4]∪[8,∞ )

Thus, minimum value of ′?′ ∀ ?∈?+ is 8.

24. The sum

$\sum _{k=1}^{20}(1+2+3+ ......+k)$

is_____________.

Solution:

$\sum_{k=1}^{20}\frac{k(k+1)}{2}$

$=\frac{1}{2}\sum_{k=1}^{20}k^{2} + k$

$=\frac{1}{2}\left [ \frac{20(21)(41)}{6}+\frac{20(21)}{2} \right ]$

=(1/2)[2870+210]=1540

25. The number of all 3×3 matrices A, with entries from the set {−1,0,1} such that the sum of the diagonal elements of (??^T) is 3, is __________.

Solution:

Let A =
$\begin{vmatrix} a_{11} & a_{12} & a_{13}\\ a_{21}& a_{22} &a_{23} \\ a_{31}& a_{32} & a_{33} \end{vmatrix}$

And A^T =
$\begin{vmatrix} a_{11} & a_{21} & a_{31}\\ a_{12}& a_{22} &a_{32} \\ a_{13}& a_{23} & a_{33} \end{vmatrix}$

(??^?)=?₁₁²+?₁₂²+?₁₃²+?₂₁²+?₂₂²+?₂₃²+?₃₁²+?₃₂²+?₃₃²=3

So out of 9 elements (???)’s, 3 elements must be equal to 1 or −1 and rest elements must be 0.

So, the total possible cases will be

When there is 6(0′?) and 3(1′?) then the total possibilities is ⁹?₆

For 6(0′?) and 3(−1′?) total possibilities is ⁹?₆

For 6(0′?),2(1′?) and 1(−1′?) total possibilities is ⁹?₆ ×3

For 6(0′?),1(1′?) and 2(−1′?) total possibilities is ⁹?₆×3

∴ Total number of cases =⁹?₆×8=672

Warning: Undefined variable $snippet_dislikes in /var/app/current/wp-content/themes/html5blank-stable/functions.php on line 2508 Warning: Undefined variable $snippet_dislikes in /var/app/current/wp-content/themes/html5blank-stable/functions.php on line 2508 Warning: Undefined variable $snippet_dislikes in /var/app/current/wp-content/themes/html5blank-stable/functions.php on line 2508 Warning: Undefined variable $snippet_dislikes in /var/app/current/wp-content/themes/html5blank-stable/functions.php on line 2508

Video Lessons - January 8 Shift 1 Maths

JEE Main 2020 Maths Paper January 8 Shift 1

JEE Main 2020 Maths Paper With Solutions Jan 8 Shift 1