What is Wave Motion?
Wave motion is the transfer of energy and momentum from one point of the medium to another point of the medium without actual transport of matter between two points. Wave motion is classified into three different ways they are,
- The medium of propagation,
- The dimensions in which a wave propagates energy,
- The energy transfer
Table of Content
Classification of Wave Motion
Based on the Medium of Propagation

Classification of Wave Motion Based on the Medium of Propagation
Number of Dimensions a Wave Propagates Energy

Classification of Wave Motion Based on the Number of Dimensions a Wave Propagates Energy
Based on the Transfer of Energy
- Standing waves (or stationary waves)
- Progressive wave
Standing waves remain confined to a region without any transfer of energy and momentum whereas the progressive waves transfer energy and momentum between the particles of the medium.
Mechanical waves (Elastic waves)
Waves that require a medium for their propagation are called mechanical waves or elastic waves. The particles of the medium execute periodic motion about a mean position when the wave propagates through the medium.
For Example, waves on a string
A mechanical wave is produced due to a disturbance at a point in a medium.
- The disturbed particle interacts with the neighbouring particle and its energy is handed over to the next particle (due to the inertia of the medium).
- The disturbed particles return to the equilibrium position (due to the elasticity of medium).
Properties of Medium for Mechanical Wave Propagation
- The medium must possess inertia so that its particles can store kinetic energy.
- The medium must possess elasticity.
- The minimum frictional force between the particles of the medium.
Non-Mechanical Waves
Waves which do not require a medium for their propagation are called a non-mechanical wave. These types of waves can propagate through vacuum also. These are transverse in nature. For example, electromagnetic waves and matter waves.
Transverse Wave Motion
The particles of the medium vibrate in a direction perpendicular to the direction of propagation of the wave. The region of maximum upward displacement is called the crest, the region of maximum downward displacement is called trough.
Transverse wave motion occurs only through a medium which has rigidity modulus or shape conservation. For example, string waves.

Longitudinal Wave Motion
The particles of the medium vibrate about their equilibrium position in a direction parallel to the direction of propagation of the wave is called a longitudinal waves.
Longitudinal waves require a medium with only elasticity of volume (or Bulk modulus) for its propagation. In this type of wave motion, the waves travel through a medium in the form of compression and rarefaction.
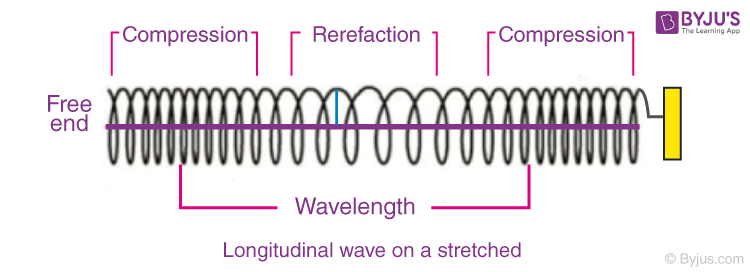
The region of high pressure is called compression and the region of low pressure is called rarefaction. For example, Sound waves in the tube.
Periodic Wave Motion
- If the disturbance is continuous and is periodic in nature, then the wave produced is termed as a periodic wave.
- A periodic wave that is varying sinusoidally is called a sinusoidal periodic wave.
- The particles of the medium execute simple harmonic motion (SHM) when a sinusoidal periodic wave passes through the medium.
Characteristics of Wave Motion
- In wave motion, the disturbance travels through the medium due to repeated periodic oscillations of the particles of the medium about their mean position (or) Equilibrium position.
- Energy and momentum are transferred from one point to another without any actual transfer of the particles of the medium.
- There is a regular phase difference between the particles of the medium because each particle receives disturbance little later than its preceding particle.
- The velocity with which wave travels is different from the velocity of the particles with which they vibrate about their mean (or) equilibrium position.
- For a given medium the velocity of the wave motion remains constant, while the particle velocity changes continuously during its vibration about their equilibrium position.
- The velocity of the particle is maximum at the mean position and zeroes at the extreme position.
Terminologies in Progressive Wave Motion
- Amplitude
- Period
- Wavelength
- Frequency
- Wave velocity
- Phase or phase angle (O)
- Phase difference
- Path difference
- Time difference
Explanation:
Amplitude (A): The amplitude of a wave is the maximum displacement of any particle of the medium from its equilibrium position.
Period (T): Period (T) of a wave is the time taken by any particle of the medium to complete one vibration during a period (T).
Wavelength (λ): Wavelength (λ) is equal to the distance between two consecutive particles of the medium which are in the same state of vibration. It is equal to the distance travelled by the wave by its time period (T).
Frequency (f): It is the number of vibrations made per second by any particles of the medium (f = 1/T). Since the frequency of a wave is a characteristic property of the source which is producing the wave motion, hence, the frequency of a wave does not change when a wave travels from one medium to another medium.
Phase or Phase Angle (Φ): It represents the state of vibration of the particle of a medium with respect to its mean position.
Phase Difference Δ(Φ): It represents the different state of vibration of a particle at two different instants (or) any pair of particles at the same instant. ΔΦ = Φ2 – Φ1.
Wave Velocity (v): It is the distance travelled by the wave in one second (v = λ/T). It is determined by the mechanical properties of the medium through which the wave propagates. The velocity of wave motion is measured with respect to the medium, the wave velocity changes when the medium is in motion i.e. speed of sound through air changes when the wind is blowing.
⇒ Check: Sound Waves
There are two velocities associated with a wave. One is the wave velocity and the other one is particle velocity (which is the speed with which the particle of the medium vibrate when the wave passes through the medium).
Path Difference (Δx) or (x): It indicates the distance between two points measured along the direction of propagation of the wave through the medium.
Time Difference (ΔT): It indicates the time taken by the wave to travel from one point to another through the medium.
The relationship between Path Difference and Phase Difference
Consider a progressive wave motion advancing in the positive direction of the x-axis

Path Difference vs Phase Difference
Let A and B be two points in the medium through which the wave passes.
The path difference between A and B is, x = x2 – x1
By the time the wave reaches B from A the phase of vibration of A has changed. The difference between the states of vibration of A and B is called phase difference (ΔO).
From this wave motion, if we consider any two consecutive crests c1 and c2, the path difference between them is λ, the time difference is T and the phase difference is 2π.
A path difference of (λ) corresponds to a phase difference of 2π, thus, a path difference (x) corresponds to the phase difference 2πr/λ.
Δϕ = (2πx)/λ = 2π/λ (path difference)
Where k = 2π/λ is called wave number or propagation constant of the wave motion.
A path difference (λ) corresponds to a time difference (T), therefore, a path difference (x) corresponds to a time difference of (x/λ)T.
The relations connecting the path difference, phase difference and time difference are given in the below table.
| Path Difference | Phase Difference | Time Difference |
| X | [2πX]/λ | XT/λ |
| λ × [Δϕ/2π] | Δϕ | [Δϕ/2π] × T |
| λ × [ΔT/T] | 2π × [ΔT/T] | ΔT |
⇒ You might also be interested in:
Waves and Simple Harmonic Motion Important Questions




good explanation