Derivation Of Schrödinger Wave Equation

Schrödinger Equation is a mathematical expression which describes the change of a physical quantity over time in which the quantum effects like wave-particle duality are significant. The Schrödinger Equation has two forms the time-dependent Schrödinger Equation and the time-independent Schrödinger Equation. The time-dependent Schrödinger Wave Equation derivation is provided here so that students can learn the concept more effectively.

Questions related to the derivation of the Schrödinger Wave Equation is one of the most commonly asked questions in board exams and various competitive exams. The derivation of the Schrödinger Wave Equation is given below in such a way that students understand the concept in an interesting and easy manner.

Schrödinger Wave Equation Derivation (Time-Dependent)

Considering a complex plane wave:

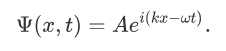
Now the Hamiltonian of a system is

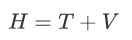
Where ‘V’ is the potential energy and ‘T’ is the kinetic energy. As we already know that ‘H’ is the total energy, we can rewrite the equation as:

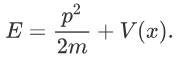
Now taking the derivatives,

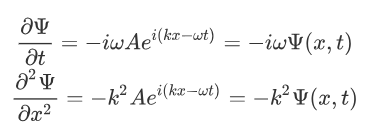
We know that,

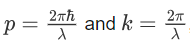
where ‘λ’ is the wavelength and ‘k’ is the wavenumber.

We have

Therefore,

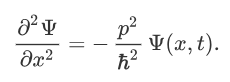
Now multiplying Ψ (x, t) to the Hamiltonian we get,

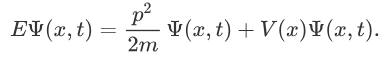
The above expression can be written as:

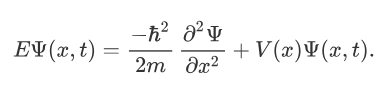
We already know that the energy wave of a matter wave is written as

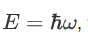
So we can say that

Now combining the right parts, we can get the Schrodinger Wave Equation.

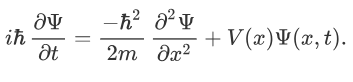
This is the derivation of Schrödinger Wave Equation (time-dependent). Students must learn all the steps of Schrodinger Wave Equation derivation to score good marks in their examination. Stay tuned with BYJU’S and learn various other derivation of physics formulas.