The line that touches the curve at a point called the point of tangency is a tangent line. Take a look at the graph to understand what is a tangent line. A curve that is on the line passing through the points coordinates (a, f(a)) and has slope that is equal to f’(a).

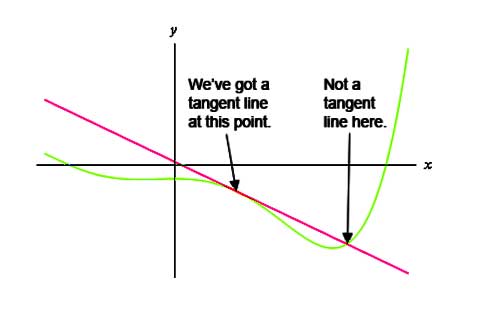
The Tangent Line Formula of the curve at any point ‘a’ is given as,

\[\large y-f(a)=m(x-a)\]

Where,
f(a) is the value of the curve function at a point ‘a‘
m is the value of the derivative of the curve function at a point ‘a‘

Solved Examples

Question 1: Find the tangent line of the curve f(x) = 4x² – 3 at x₀ = 0 ?

Solution:

Given:
f(x) = 4x² – 3
x₀ = 0

f(x₀) = f(0) = 4(0)² – 3 = -3
f'(x) = 8x
m = f'(x₀) = 8(0) = 0

The tangent line formula is,

y – f(x₀) = m(x – x₀)
y + 3 = 0(x – 0)
y = -3

The tangent of the curve is, y + 3 = 0